Quelques bateaux…

Saurez-vous retrouver toutes les fonctions utilisées pour réaliser ces différents dessins ?

Travail réalisé par Michaël S., Laurent M. et Marc M. :

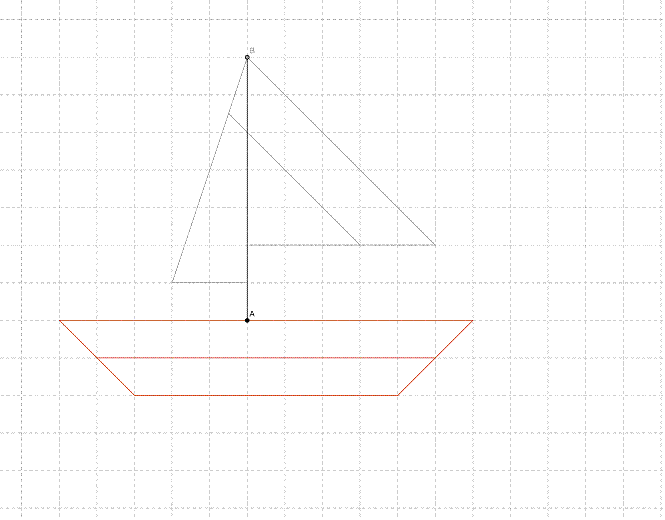
Dans un repère orthonormé, les points A et B ont pour coordonnées respectives (0 ; - 0,5) et (0 ; 3).

Nous avons tracé le segment [AB] puis exclusivement des représentations graphiques de fonctions affines.

Notre démarche :

Lorsque la fonction que l’on doit utiliser est décroissante, le coefficient directeur de la droite qui la représente est négatif. Sinon, il est positif.

Pour trouver ce coefficient, nous avons tout d’abord cherché l’intervalle sur lequel sera définie la fonction affine puis les coordonnées des points C et D extrémités du segment à tracer. Il suffit d’appliquer la formule suivante : (Yd-Yc)/(Xd-Xc) = coefficient directeur.

Ensuite il suffit de remplacer X par Xc et Y par Yc pour trouver l’ordonnée à l’origine de la droite.

Travail réalisé par Marc P., Camille B. et Claire G. :

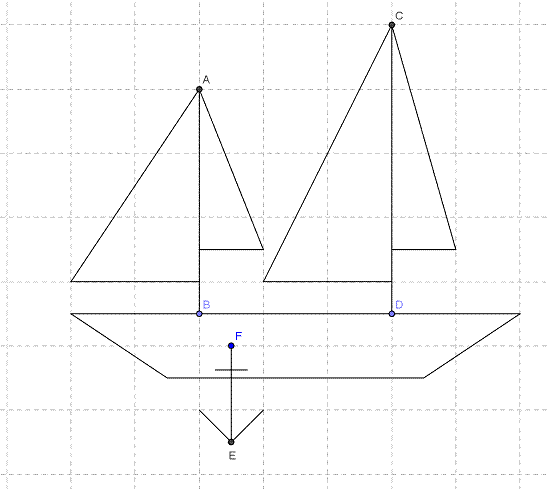
Dans un repère orthonormé, les points A et B ont pour coordonnées respectives (-2 ; 6) et (-2 ; -1).

Nous avons tracé plusieurs segments : [AB], [CD] et [EF]. Excepté ces trois segments, tous les autres sont des représentations graphiques de fonctions affines.

Notre démarche :

Après une longue recherche pour retrouver la formule de calcul, nous nous sommes souvenus qu’il fallait calculer le coefficient directeur (a = (y_B-y_A)/(x_B-x_A)) puis nous avons remplacé a dans y = ax+b, ce qui nous a permis de trouver l’ordonnée à l’origne (b = y – ax). Nous avons, ensuite, mis sur « pied » notre bateau.

Travail réalisé par Sophie R. et Anaïs M. :

Dans un repère orthonormé, les points A et B ont pour coordonnées respectives (1 ; 5) et (1 ; -1,5).

Notre démarche :

Nous avons placé ensuite tracé tous les segments « obliques » ou horizontaux qui forment le bateau. Nous avons noté leurs coordonnées et avons ensuite, pour déterminer l’équation réduite de chaque segment, résolu un système de deux équations linéaires à deux inconnues, en utilisant le fait que l’équation du segment est de la forme y=ax+b et que les coordonnées des deux extrémités vérifient cette équation.