« Une voile à l'horizon »

Malik, Thomas, Sara, Morgane

Debout face à la mer, un mathématicien hésite à se jeter dans les vagues: finalement, l'eau n'est pas si chaude... Il regarde la mer qui s'étend jusqu'à la ligne d'horizon, où le ciel bleu clair rencontre la mer bleu foncé. À ce moment précis, un hors-bord disparaît derrière la ligne d'horizon. À quelle distance est-il du mathématicien ?

Les marins avaient l'habitude d'envoyer un matelot -la vigie- en haut du mât, pour surveiller la mer sur une grande étendue. Jusqu'à quelle distance la vigie pouvait-elle observer la mer ?

Un voilier apparaît à l'horizon, le mathématicien voit d'abord la voile, puis bien plus tard, la coque du voilier. À quelle distance est le voilier quand le mathématicien commence à voir la voile à l'horizon ?

À quelle distance est-il quand il peut distinguer la coque?

(Les premières questions sont traitées par Thomas et les deux autres par Morgane)

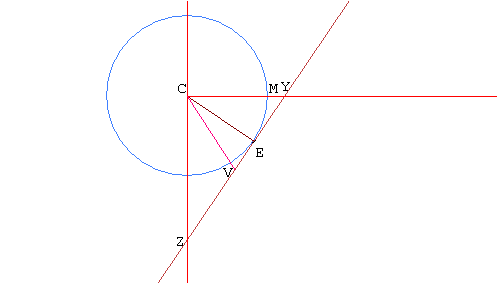
La terre est représentée par le cercle de centre C et de rayon [CE]. Le point V correspond aux yeux du mathématicien. [MY] désigne le mât du voilier.

Jusqu'à quelle distance la vigie pouvait-elle observer la mer ?

D'après le théorème de Pythagore dans le triangle CEY rectangle en E :

(rayon de la terre+taille du mât)² – (rayon de la terre)² = (distance jusqu’à laquelle peut observer la vigie)²

En remplaçant par les mesures connues (en mètres) on obtient :

(6400000+15)² – (6400000)² = 192000,225

√192000,225ó 13856

13856 m = 13,856 km soit environ 14 km.

La vigie peut donc observer à 14 km à la ronde environ.

Pour la partie qui suit, nous étions seulement deux donc le travail à été sensiblement plus difficile. On ne voyait pas exactement quel calcul effectuer sinon le même que pour la première question puisque si le mathématicien voit la voile, c'est qu'elle est pile sur la ligne d'horizon mais après plusieurs relectures de l'énoncé, nous avons remarqué que la voile est à une hauteur de 15m donc les calculs étaient forcément différents. Pour la toute dernière partie, il n'y a pas vraiment eu de difficultés puisque si il voit la coque, et que nous considérons qu'elle est au ras de l'eau, c'est qu'elle vient de passer la ligne d'horizon donc nous sommes revenu au premier calcul effectué dans l'exercice.

 À quelle distance est le voilier quand le mathématicien commence à voir la voile à l'horizon ?

Nous savons que le rayon de la Terre est égal à 6400 km mais pour plus de précision, nous allons faire tous nos calculs en mètres, soit le rayon de la Terre = 6 400 000 m.

Nous avons utilisé le théorème de Pythagore dans le triangle rectangle CEY:

YE² =(rayon de la Terre + hauteur de la voile)² - (rayon de la Terre)²

En remplaçant pas des valeurs, nous avons trouvé:

YE²=(6 400 000+15)² - (6 400 000)²= 192 000 225

YE=√(192000225)ó13,8 km

Ensuite, nous avons ajouté la valeur trouvée dans la première partie, qui donne la distance du bateau avec le mathématicien, soit VEó4,7 km et avons trouvé environ 18,5 km.

Donc, quand la voile apparaît, le voilier et à 18,5 Km du mathématicien.

À quelle distance est le voilier quand le mathématicien peut distinguer la coque?

Nous considérons donc que la coque du bateau est au ras de l'eau donc c'est comme si nous cherchions la distance qu'il y a entre le bateau et le mathématicien, soit 4,7 km