« Une voile à l’horizon »

Emilie R. & Antonin T.

Debout face à la mer, un mathématicien hésite à se jeter dans les vagues : finalement, l’eau n’est pas si chaude … Il regarde la mer qui s’étend jusqu’à la ligne d’horizon, où le ciel bleu clair rencontre la mer bleu foncé. A ce moment précis, un hors-bord disparaît derrière la ligne d’horizon. A quelle distance est-il du mathématicien ?

Les marins avaient l’habitude d’envoyer un matelot -la vigie- en haut du mât, pour surveiller la mer sur une grande étendue. Jusqu’à quelle distance la vigie pouvait-elle observer la mer ? Un voilier apparaît à l’horizon, le mathématicien voit d’abord la voile, puis bien plus tard, la coque du voilier. A quelle distance est le voilier quand le mathématicien commence à voir la voile à l’horizon ? A quelle distance est-il quand il peut distinguer la coque ?

Remarques :

- Le rayon de la Terre est de 6 400 Km

- Un mathématicien mesure en moyenne 1m80 et quand il est debout, ses yeux sont à 1m70 du sol

- Le mât d’un bateau mesure 15 m

Pour réaliser cet exercice, nous avons surtout peiné au début, car on n’avait pas fait de dessin et c’était difficile pour nous de s’imaginer la situation. Mais une fois le dessin fait, tout a découlé et c’était beaucoup plus simple.

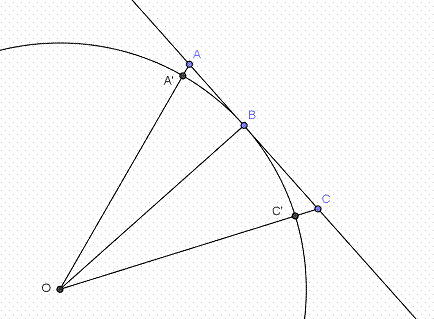
La terre est représentée par le cercle de centre O et de rayon [OB]. La longueur AA’ représente la distance séparant les yeux du mathématicien au sol à savoir 1,70 m. La longueur CC’ représente la hauteur du voilier à savoir 15 m.

A quelle distance le hors-bord est-il du mathématicien ?

On a le triangle ABO rectangle en B, on peut alors appliquer le théorème de Pythagore :

AB²=AO²-BO²

AB²=((6 400.10³)+1,70)²-(6 400.10³)²

AB²=21 760 002,8

AB=4 664,8 m

AB=4,66 Km

Le bateau est à 4,66 Km du mathématicien.

Jusqu’à distance la vigie pouvait-elle observer la mer ?

On a toujours le triangle OBC rectangle en B, on peut appliquer le théorème de Pythagore :

CB²=OC²-BO²

CB²=((6 400.10³)+15)²-(6 400.10³)²

CB²=192 000 225

CB=13 856,4 m

CB=13,8 Km

La vigie pouvait observer la mer jusqu’à 13,8 Km.

A quelle distance est le voilier quand le mathématicien commence à voir la voile à l’horizon ?

On veut savoir à quelle distance le mathématicien commence à voir la voile à l’horizon. Sachant qu’il peut voir la ligne d’horizon situé à 4,66Km, on ajoute cette valeur à la précédente. On obtient donc la distance 18,4Km.

Quand le mathématicien commence à voir la voile, le voilier est à 18,4 Km.

A quelle distance est-il quand il peut distinguer la coque ?

Le mathématicien peut distinguer la coque du voilier à 4,66 Km car la coque est au niveau de la ligne d’horizon c'est-à-dire comme le hors-bord, à la même distance.